What a difference a Year makes!

May 22, 2025 – 7:01 AM

These are just some of my personal takeaways from Computex 2025 here in Taipei, Taiwan. This is not a comprehensive review of the mother of all Asian trade shows, just some notes about things I’m interested in. I got to attend Jensen Huang’s keynote speech this year. Wow, what a difference a year makes! Last year the hype was on full bore, announcement of the Blackwell GPU’s and all kinds of possible applications for AI, a few were pretty creepy to some folks, but mostly all just smoke and mirrors.

This year there was none of that. The presentations (and Huang himself) were considerably more subdued, but instead of hype we actually saw real hardware, real applications and real results from applied AI, particularly Nvidia’s Omniverse, their operating system for 3D simulation.

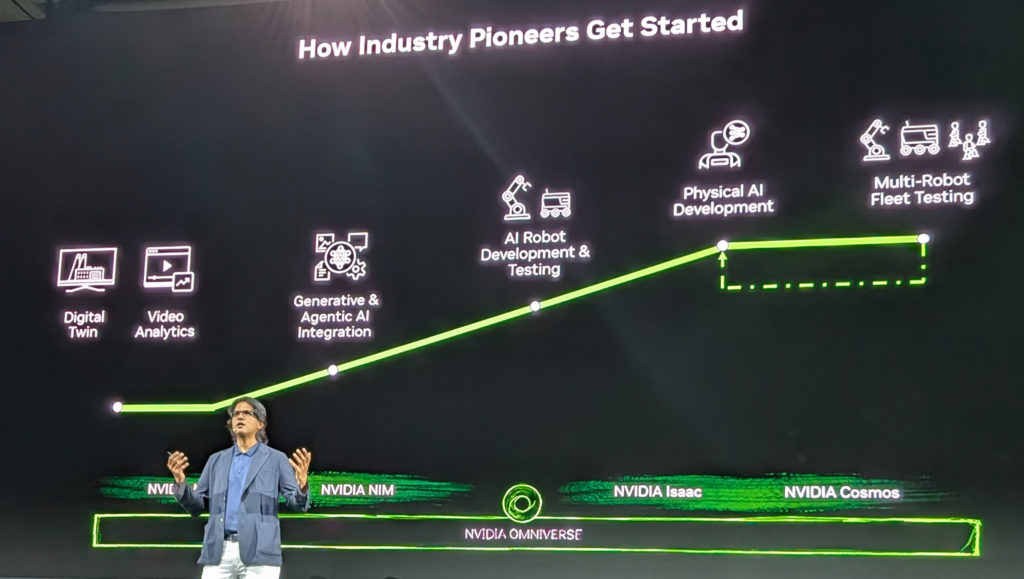
Deepu Talla from Nvidia said that physical AI and 3D simulation have reached a tipping point. Nvidia Omniverse is the operating system for simulation of physical problems. This combination of physical AI and simulation has come about within the last 12 months. Foundation models for robotics physics are very limited currently. Synthetic data generation is needed to aid simulation. Robotics needs extremely accurate data. Using generative AI can generate the data, while Omniverse combines synthetic data with real world data in order to drive robots. Robots gather real world data with sensors in order to improve their performance. He noted Foxconn’s use of Omniverse to simulate the design of new factories was probably the largest deployment of Omniverse to date.

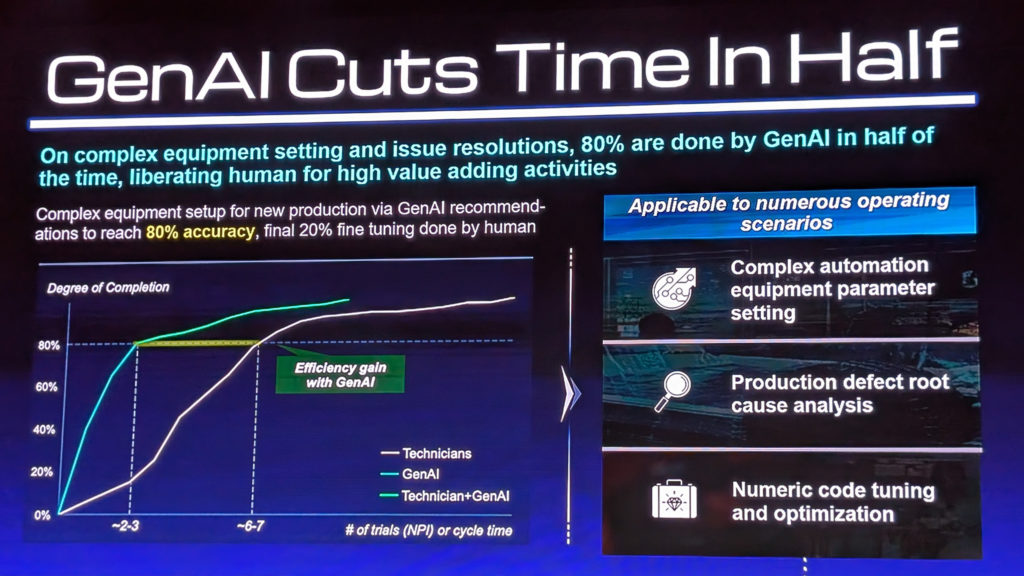
Foxconn’s chairman, Young Liu, described in detail in a forum after Huang’s keynote how Foxconn has used Omniverse to simulate designs of their factories. The creation of a fully synthetic simulation “digital twin” of a factory helps implement not only the building and equipment layout but also simulation of how the robots that are needed will work and then using the results of simulations to actually program those robots. This saves months of planning and construction time. Foxconn’s goal is to have robots do 80% of tasks while 20% of remaining tasks beyond robotic capabilities are done by humans. Labor shortages are driving Foxconn’s deployment of robots. All this has taken place within the last year and a half. Young says the great challenge for countries is the replacement of low GDP work with generative AI as the world is running out of low GDP countries.

Ed H. Chi from Google noted that Google Gemini has gone from processing 9.7T (terra-tokens) per month to 480T tokens per month in just one year. Referring to the Google Deepmind project, in the past separate models were required depending on each task at hand. But now all of these models have been compressed into a single large model. Maybe this is just marketing hype, but Chi claims this is the biggest advance in computer science in the last 10 years.

Jens Hinrichsen from NXP said that physical AI has to move to the “edge” because of all the data being generated. AI plus IOT is the way forward. Context processing at the edge is needed to extract the true value from data and discard that which is of no value, much like the way our brains work. There’s simply not enough internet bandwidth to send everything from the edge to the cloud for processing there.

Within the last year Agenic AI has become a reality- edge devices have become autonomous, there’s no need for the cloud in order to allow edge devices to sense, think and act on their own. But the edge and the cloud will always coexist. AI agents can learn and adapt to situations. But a very large challenge is providing a high level of control reliability, safety and cyber security.

I think the real “killer app” for AI has finally become obvious: management of vast amounts of data in order to extract value. “Digital Twin” is not exactly a new concept, we’ve been doing that for many years in product development, creating a fully synthetic 3D functioning model of a product before cutting any tooling. But doing it on this kind of scale and enabled with AI plus physical data is new. It’s nice to see genuine high value applications finally emerging at last from all the past hype around AI. However, the 800 pound elephant in the room is still with us. Power requirements to run AI “factories” are outpacing the planet’s ability to generate electricity. Last year’s Nvidia Grace Blackwell 100KW rack has morphed into this year’s Blackwell 160KW rack. Even edge devices are becoming more power hungry as their processing power increases. Those of us in Taiwan, where they’ve just shut down the nation’s last nuclear reactor, may soon have to make hard choices between AI and AC.

By admin | Posted in Simulation | Tagged , | Comments (0)

Why Oboes Crack

April 20, 2016 – 6:00 PM

The "White Heron" castle of Himeji

The “White Heron” castle of Himeji

Before we even begin discussing why instruments crack the number one question on your mind right now probably is “Can I absolutely prevent my instrument from cracking?” The answer unfortunately is ‘no’, BUT there are things that can be done which greatly reduce the likelihood that an instrument will crack. I will caution you right now that there are many opinions about how to prevent cracking and how to properly care for a wooden instrument, not all of which are grounded in an understanding of how wood works.

African Blackwood (grenadilla) tree trunk cross section

African Blackwood (grenadilla) tree trunk cross section

The wood which most oboes is made from comes from the African Blackwood tree. It’s also called grenadilla wood, and is similar to other deciduous hardwoods. The section of the tree used for instruments is the center of the trunk, the heartwood. The tree when lumbered is usually cut up into billets of various sizes, taken from the best of the heartwood. Since these trees don’t grow very straight the number of useable billets from each tree is fairly low, one of the reasons the wood is so expensive. It’s just like making reeds where 99% of the harvested cane is eventually thrown away in order to get to decent tubes.

Blackwood billets after lumbering

Blackwood billets after lumbering

To understand why instruments crack we need to first take a look at how wood behaves under different circumstances. Let’s look at a blackwood billet, see illustration below:

Wood5

Note that the grain direction always runs in the same direction as the tree trunk. This is also the major strength axis of the wood. For example, if you were to attempt to split the piece illustrated above in two by striking it with an axe on the end or on the side in the same direction as the grain it would split apart with little effort. But striking the wood across the grain on the side yields nothing but frustration as it will not yield in that direction. Wood is porous and will easily absorb moisture on the ends due to capillary action. It will also absorb moisture through the sides across the grain but not as readily. It’s critical to note here that wood is NOT dimensionally stable across its width, that is, across the grain. Very little expansion and contraction due to moisture occurs along the wood in the direction of the grain, but across the grain the movement is significant, driven primarily by the moisture content of the wood, and to a lesser degree by its temperature.

When a tree is harvested and lumbered, there is a significant amount of moisture in the wood, usually much higher than the surrounding ambient humidity. Before wood can be made into instruments, it must be properly “seasoned”, that is, allowed to reach a stable moisture content. For furniture making a moisture content by weight of around 7% is considered ideal, so to season wood properly it must be stored for several years in an atmosphere of around 35% to 40% relative humidity. Because of the density of African blackwood typical seasoning times are at least 5 years. Once an instrument is machined from billets of blackwood the machining process itself can relieve stresses built up in the wood created whilst the tree was growing. Sometimes these stresses take time to work themselves out after all the machine work is done, resulting in slight dimensional changes to the instrument. This is one reason why there are no two oboes which are exactly alike even though they were made at the same time from the same batch of wood, even from the same tree.

So back to your original question, how do we keep our oboes from cracking? We must do things that minimize wood movement. Since it’s impractical to prevent all wood movement we need to learn to deal with it so that it does not cause cracking. M. Alain de Gourdon of F. Lorée says that cracking typically occurs in cold and dry places around the world. In North America, instruments are particularly at risk because we tend to overdo forced air heating and air conditioning, both of which greatly reduce humidity and can create dangerous extremes of humidity and temperature from one location to the next.

F. Lorée ships a set of instructions with every new instrument on how to properly “break it in”. Following those instructions carefully will greatly reduce the likelihood of cracking:

“The following will help you to get the most enjoyment from your new instrument and reduce the possibility of cracking. The risk can be minimized by playing the new instrument gently during the first few months, and by taking precautions during periods of low humidity.

In the beginning, play the instrument for no more than 10-15 minutes at a time. Swab it, return it to its case and keep the lid closed. A few hours later or the next day, you may repeat this procedure. Each week you may add five to ten minutes playing time. After about three months, you should be able to play it as you wish.

On chilly days (or in cold rooms) always warm the instrument before beginning to play on it. This may be done by holding it against your body for a few minutes, or cradling at least the top joint in your hands. If the oboe was left in an unheated area on a cold day, you must not play it until it has had a chance to warm gradually. [emphasis mine]

Avoid laying down the instrument on a cold or very warm surface or next to a heat source so that it is not exposed to rough variation of temperature. If your instrument is kept in a dry climate, or even during prolonged periods of dry weather, the best is to put a humidifier in the case to maintain higher moisture.

During the break in period, we recommend you to oil regularly the bore of your new instrument (about once a week). Be sure first, that the bore is well dried and cleared of moisture. Then put some drops of “F. Lorée” natural bore oil preferably on a feather and apply a light coat of oil gently inside the instrument. After a few months, you can progressively reduce to oil your instrument.”*

* From instruction sheet shipped with every new Lorée instrument, courtesy of Alain de Gourdon, F. Lorée

M. Alain de Gourdon recommends the use of their natural bore oil or natural almond oil. The idea behind oiling the bore is to reduce the wood’s ability to absorb moisture from your breath that condenses in the bore. Repeated oiling gradually infuses oil into the wood, displacing some of moisture that is there and preventing it from picking up additional moisture from your breath. Ideally at some point the oil will have displaced most of the moisture in the wood such that changes in ambient humidity and temperature will have a significantly less effect on wood movement, greatly lowering the risk of cracking. Also, don’t do dumb things like leaving an instrument in the car where it can overheat and crack in the summer or get chilled in winter. Outside in the winter keep your instrument under your coat. Always use an insulated case.

Oiling an oboe:

Refer to the instructions provided by F. Lorée listed above. Be sure the oboe is dry on the inside before oiling. Do not try to oil right after playing. Use a feather long enough to go through the top joint and stick out of the reed well when you feed it base first from the bottom. This might seem rather cumbersome BUT it keeps the feather from poking into the tone holes and leaving excess oil there which it surely would if you pushed it through from the joint. Put just 2 or 3 drops of oil on the end of the feather, then slowly pull it through while twisting it. Repeat this several times to spread the oil around but don’t add any more oil after the first pass. Feathers work best at spreading the oil around as they won’t absorb the oil. Viewing the bore against a light from the top the inside should be slightly shiny from the oil, but not soaking wet. Note that the first time you oil a new oboe the oil will soak in almost immediately. Keep tone holes pointed up throughout this process to keep oil from pooling in them. Oil can make pads stick so keep it out of the tone holes. After oiling, put the oboe away and let it rest for at least 24 hours to allow time for the oil to diffuse. Oil the bottom joint in the same manner. The end of the bell with all of its exposed end grain will absorb a lot of oil so the best way to oil the end of the bell is to put a drop or two of oil on your finger and rub it in, much like finishing fine furniture. A little bit of oil goes a long way. Too little is better than too much, especially after the first time. I also apply a small amount of oil to the wood under the thumb rest and the first octave key since these areas can absorb a significant amount of moisture from your thumbs.

The use of natural almond oil was mentioned. This is also known as sweet almond oil and is usually available at any health food store or natural market. This is a cosmetic grade (as opposed to food grade) oil. Cosmetic grade oil has stabilizers in it which keep it from getting rancid or gummy. Petroleum based oils should be avoided, these can cause the wood to deteriorate. Vegetable oils should be avoided as well as these will eventually get rancid and gummy. When in doubt use F. Lorée natural bore oil. You should continue to use only the kind of oil that was first applied to the instrument for all future oilings.

Years ago oboe players tended to keep their instruments for much longer periods than professional players do now. The legendary English oboist Leon Goosens played on the same USED Lorée oboe for 40 years and it never cracked. But he was a little extreme in the care of his instrument. Once a year he would remove all of the key work and thoroughly oil it inside and out. He would then allow it to rest to let the oil soak in before reassembling and adjusting it. That’s definitely over the top for most of us. Over oiling an instrument is not a good thing. If there’s too much oil in the wood it will tend to ooze out and cause pads to stick. There is no way to remove excess oil from the wood, so don’t overdo it.

If left to acclimate properly an oboe will be perfectly happy in a tropical country, but in colder climates some effort may be needed to maintain a minimum level of moisture content in the wood. There is a lot of FUD surrounding the use of humidifiers in one’s instrument case. Some people even put orange peels and other silly things in their cases in order to raise the humidity inside. Don’t do that. Only use a device specifically designed to perform this task. Remember that humidification is called for only if the instrument will be kept for long periods of time (more than a day or two) in an environment where the relative humidity is low. In North America relative humidity indoors in the winter can drop to 20% or below due to excessive heating. A humidifier is called for if the humidity in the environment where the instrument is stored is below 40%. As with oiling, humidification can be over done. Excessive moisture will cause the wood to swell, leading to all kinds of unwanted movements, possibly even cracking. The sound will be affected as well.

Why oboes crack:

Note that an instrument will take up moisture somewhat more quickly than it will release it, which is why it’s so important to oil it and to control extremes of temperature and humidity that an oboe is exposed to. Cracks occur due to a buildup of stress in the wood because of differences in moisture content and temperature between the bore and the outside surface of the oboe, almost always in the top joint. The top joint is particularly vulnerable to cracking due to its smaller overall diameter than the bottom joint, the greater difference between the inside (bore) diameter and the outside diameter, and higher temperature saturated air from the player’s breath, which is much cooler by the time it reaches the bottom joint.

Relative cross sections of the top joint (left) and lower joint.

Relative cross sections of the top joint (left) and lower joint.

Warm moist air passing through the top joint diffuses moisture into the sides of the bore, and along with the warmth causes the wood to swell. Compression stresses build up in the center and work their way outward against tension forces from the outside in until something gives and a crack opens up.

Crack formation in the top joint

Crack formation in the top joint

This is why cracks usually appear on the outside surface and may not work their way through to the bore. Remember that across the grain of the wood is the weakest strength axis, which is why cracks typically form along the length of the top joint or between the tone holes. Reducing moisture absorption in the bore goes a long way to help prevent cracks, hence the need to oil early and often in the life of a new instrument, and to carefully maintain its environment.

Post copyright (c) 2016 Jeffrey W. Sutherland.  All rights reserved.

By admin | Posted in Double Reed Instruments | Comments Off on Why Oboes Crack

Could Most Of What You Think You Know Be Wrong?

March 27, 2016 – 10:29 PM

Hiroshima_night

Hiroshima night scene

When preparing for a Value Analysis study keep that thought in mind.  One of the principal roadblocks to finding good value is “We’ve always done it that way”.  There are a number of others, and note that eliminating roadblocks is one of the principal challenges when conducting a value analysis kaizen.  Along with the roadblock “We’ve always done it that way” is conventional wisdom born of tribal knowledge in the organization.  There is a natural resistance to change.  Accepting long held beliefs as true or relevant is simply because thinking is hard work for most people.  There may be cultural issues to deal with as well.  In America there are varying amounts of pressure to conform in most organizations, and no one wants to rock the boat.  In other cultures, particularly in Asia, the pressure to conform is much greater. In China, especially when trouble shooting production problems, it’s extremely difficult to get to the bottom of things because above all else people there make every attempt to avoid getting blamed for something, and avoid laying blame anywhere else.  I once was in a meeting with a room full of workers in China who were dealing with a problem with a batch of parts that were failing incoming inspection.  These blokes went round and round for an hour and a half and got nowhere.  During a bathroom break whilst waiting for them to return I picked up the item in question and took a close look at it for the first time and realized immediately that the supplier had made the part with worn out threading dies.  When I pointed this out when everyone returned, only after another hour’s worth of discussion and a trip to the optical comparator everyone finally agreed that the problem lay with the supplier.  But they were definitely loth to admit that.

Another principal tenet of value analysis is using the best possible data available.  Everyone is making the wrong argument about so-called global warming.  Of course the climate is changing.  The climate has always been changing, either getting warmer or getting cooler, but never static.  The fact that a mild warming period that began in the 1700’s roughly coincides with the industrial revolution and increase in population has the climate change activists blaming this warming on human activity.  As a dynamic but mostly stable system the earth’s climate seems most heavily dependent on one single factor: the output of the sun.  As far as the proportion of the current warming trend attributable to human activity it seems, compared with other factors, to be insignificant.  Given the thermal mass of all the water in the oceans, the atmosphere and the earth itself, compared to the annual output of all fossil fuel burning worldwide that massively overwhelms anything that humans could possibly do.  Except maybe for cities, which seem to contribute significantly to warming, at least where I live.  It’s always at least 5 degrees cooler here in the country than in town.  If heat is the problem then why is no one talking about what some climate scientists have theorized- that we will be entering a period of global cooling sometime around 2030?  But where is the data?  What effect does human activity have on the climate anyway?  Nobody can put a number on it.  Anecdotal evidence does not count when performing value analysis.  When politicians threaten legal action against so-called climate change deniers we can be sure it’s not about climate science, it’s about money and power, pure and simple.

Think about some doom and gloom predictions from the not too distant past.  Remember back in the 1970’s how many said the world was going to run out of food?  Then the green revolution happened.  Remember also from that time the population explosion alarmists and the predictions of 10 billion or more people?  Just the opposite is occurring.  As countries develop and become more wealthy people naturally have fewer children.  Most developed countries around the world now have population growth below replacement rates.  This is a huge looming disaster for countries like Japan, slated to lose HALF its population by 2060, and South Korea, whose population could fall proportionately even more.  China recently eliminated its one child policy but not likely soon enough to prevent population decline there as well.  Oh, and about all that noise we’ve heard for at least 50 years about “peak oil” and the fact that we’re running out of it?  One of the biggest problems today with oil is where to store it all.  Idle railroad tank cars are sitting on sidings full of the stuff simply because there is nowhere else to put it.  Soon the USA will be the world’s largest oil producer, surpassing even Saudi Arabia.

Think of what we eat in America and about how wrong all the recommendations from the government about nutrition have been.  Actually it should not be surprising since a lot of this so-called dietary guidance is promoted by processed food makers, most of whose products are making people sick.  But everything you know about what and how to eat is probably wrong, or at least highly misinformed.  Drink several glasses of milk a day?  Wrong.  Butter is bad for you because it has fat? Wrong. The list is too long to go into here.  But if we can’t seem to get even basic things like how to eat properly right, what other generally held beliefs that we all have might be not quite so or totally the opposite?  Don’t ever be afraid to question anything. But do your research carefully and consult multiple sources.  Question everything.  Get the best data available.  Find qualified subject matter experts to join the value analysis team.  The most significant cost reductions usually come from areas that you least expect to yield savings.  That’s one of the greatest features of the Value Analysis methodology.

By admin | Posted in Uncategorized, Value Analysys | Comments Off on Could Most Of What You Think You Know Be Wrong?